11726번: 2×n 타일링
2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오. 아래 그림은 2×5 크기의 직사각형을 채운 한 가지 방법의 예이다.
www.acmicpc.net
문제
1x2, 2x1 타일로 2xn의 칸을 채우는 문제. 1x2 하나만 놓을 수는 없으므로 결국 2x2, 1x1 타일을 놓는 경우의 수가 된다.아, 근데 경우의 수를 10,007로 나눈 나머지를 출력해야 한다.
중복되는 부분 문제
개인적으로 문제는 처음 문제를 접했을 때, 답이 너무 보이지 않았다. 여느 DP 문제처럼, 2xn 타일은 더 작은 타일을 합쳐서 만들 수 있다는 점을 이용해서 풀 수 있는데, 2 x n 타일링은 2 x (n-1)에 2x1 타일을 붙이거나, 2 x (n-2)에 2x2 타일을 붙여서 만들 수 있다. 그림으로 살펴보자.
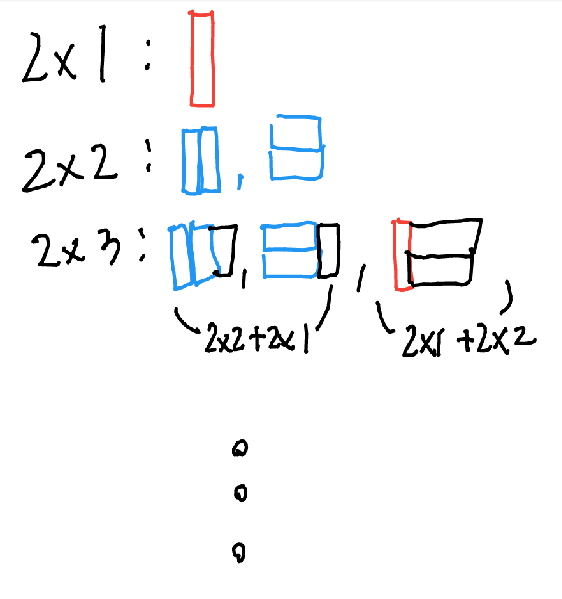
따라서 다음과 같은 점화식으로 문제를 풀 수 있다. d[n] = d[n-1] + d[n-2]
다른 해석
다른 해석? 이라고 하긴 애매하지만 일단 써본다. 이 문제는 1, 2, 3 더하기와 매우 유사한데, 이 문제는 1, 2 더하기 정도로 생각할 수 있다. 즉, (1x2, 2x2 타일로 2xn 타일을 만드는 경우의 수) = (1, 2를 더하여 n을 만드는 경우의 수)가 성립한다. 2x5 타일의 개수를 그림으로 한 번 그려보면서 구해보자.

2x5 타일은 2x4에 2x1을 더했거나, 2x3에 2x2를 더한 것이다. 또, 2x4는 2x3에 2x1을 더했거나 2x2에 2x2를 더한 것이다. 이런 식으로 쭉 거꾸로 내려가면서 더 이상 뺄 수 없을 때까지 빼다 보면 위와 같은 트리가 그려진다. 위 그림과 1, 2, 3 더하기에서 그렸던 그림이 매우 유사하다.
구현
'Algorithm Theory > Dynamic Programming' 카테고리의 다른 글
| [DP] [BOJ 1003] 피보나치 함수 (0) | 2020.03.22 |
|---|---|
| [DP] [BOJ 1149] RGB거리 (0) | 2020.03.20 |
| [DP] [BOJ 9095] 1, 2, 3 더하기 (0) | 2020.03.18 |
| [DP] [BOJ 1463] 1로 만들기 (0) | 2020.03.18 |
| DP 백준 문제 풀이 (0) | 2020.03.18 |



댓글