이번 글에서는 네트워크 유량 문제 (네트워크 플로우)와 포드 풀커슨 알고리즘에 대해 알아보자.
네트워크 유량 문제 (Network Flow Problem)
원래의 그래프는 간선을 거리, 비용으로 생각했다면, 유량 네트워크 (Flow Network)에서는 단방향 그래프에서 간선의 가중치를 최대로 흐를 수 있는 용량(capacity)과 실제로 흐르는 유량(flow)으로 생각한다. 이게 무슨 말이냐 하면 A에서 B로 가중치가 10이 존재한다면, A에서 B로 흐를 수 있는 최대 물의 양이 10이라고 해석할 수 있다. (실제로 물이 얼마나 흐르는지는 우리가 얼마나 흘려보내냐에 따라 다르다.)

이제 유량 네트워크가 뭔지 대충 느낌을 알았는데, 그래서 네트워크 유량이 뭐냐? 하면 네트워크 유량은 이 유량 네트워크에서 최대로 물이 얼마나 흐를 수 있는가?를 구하는 문제이다. 이때 흐를 수 있는 물의 양을 최대 유량(Max Flow)이라고 한다. (아까부터 물이라고 했는데, 물, 데이터, 기름 등 뭐든지 흐를 수 있는 것이면 된다. 일반적으로 통틀어서 그냥 "유량이 흐른다"라고 표현한다.)
또한 네트워크 유량 문제는 "어디에서 어디로 최대 얼마만큼의 유량이 흐를 수 있는가?"라는 문제이므로 "어디에서"와 "어디로"가 중요한데, "어디에서"를 source라고 하고 "어디로"를 sink라고 한다. 위 그림에서는 A가 source, B가 sink이다. 그런데 source, sink 모두 용어가 s로 시작하므로 보통 source를 $s$로, sink를 $t$로 표기한다.
포드 풀커슨 알고리즘 (Ford-Fulkerson Algorithm)
포드 풀커슨 알고리즘은 최대 유량을 구하는 알고리즘이다. 알고리즘이 아니라 방법론(Method)라고 부르기도 하는데, 이는 뒷부분에서 언급하겠다.

포드 풀커슨 알고리즘을 완성하기 위한 정의들
residual capacity (잔여 용량, 남은 용량) : $c_f(u, v) = c(u, v) - f(u, v)$
정점 u에서 정점 v로의 잔여 용량은 최대 용량에서 실제 흐르는 양을 뺀 것이라는 의미이다. 위의 그림에서는 용량이 10, 유량이 7이라고 했으므로 잔여 용량 = 용량 - 유량 = 10 - 7 = 3만큼의 유량이 더 흐를 수 있다.
skew-symmetricity (반대칭성) : $f(u, v) = -f(v, u)$
반대칭성은 아까 그림에서 A->B에서 7의 유량이 흐른다면, B->A로는 -7의 유량이 흐를 수 있다는 것을 의미한다. 유량이 음수인 게 무슨 개소리냐? 고 할 수 있겠지만 이게 포드 풀커슨의 킬링 포인트인데, 반대칭성의 정의를 이용하면 B->A로의 잔여 용량은 $c_f(B, A) = c(B, A) - f(B, A) = 0 - f(B, A) = f(A, B) = 7$ 식을 정리하면 $c_f(B, A) = f(A, B)$이다. 정리된 식을 해석하면 B->A 방향으로는 A->B방향으로 흘러 보낸 만큼 다시 되돌릴 수 있다. *다시 말해, 이미 유량을 흘려보냈던 행위를 취소할 수 있다.
residual network (잔여 네트워크) :
잔여 용량을 가중치로 갖는 그래프를 의미한다. 위의 그림을 예시로 들면 A->B로의 잔여 용량은 3이다. A에서 B로 3만큼의 유량을 흘려보낼 수 있다. 또한 B->A로의 잔여 용량은 7이다. 따라서 7만큼의 유량을 되돌려 보낼 수 있다. 가중치가 이렇게 잔여 용량으로 이루어져 있다.
포드 풀커슨 알고리즘을 완성하기 위한 성질들
capacity constraint (용량 제한) : $0 \geq f(u, v) \leq c(u, v)$ (유량은 0 이상 용량 이하)
flow conservation (유량 보존) : source, sink를 제외한 모든 정점에서는 들어오는 유량과 나가는 유량이 같다
포드 풀커슨 알고리즘의 진행 과정
자, 아직 이 알고리즘이 어떻게 동작하는지도 모르는데 벌써 많은 개념을 배웠다. 이제 진행 과정을 살펴보자 크게 두 단계로 나뉜다.
1. BFS or DFS로 잔여 네트워크에서의 source에서 sink로의 경로를 찾는다 (이를 augumenting path라고 한다. 추후에 다시 설명하겠다.) (단, u->v로의 잔여 용량이 0 이상인 경우에만 경로가 만들어질 수 있다.) 당연한 말이지만 이미 파이프가 꽉 차면 더 이상의 유량을 흘려보낼 수 없다.
2. 앞에서 찾은 경로를 이루는 간선 중 잔여 용량이 가장 작은 것을 찾는다.
3. 2에서 찾은 것을 전체 유량에 더해준다
4. 1~3을 다시 반복
이 과정을 통해서 구한 유량의 총합이 최대 유량이 된다.
그런데 아마 저 세줄로 이 알고리즘을 이해하긴 어려울 것이다. 그러므로 예시를 살펴보자.

앞서 말했듯 DFS, BFS 중 무엇을 써도 상관없고 임의의 경로를 선택해도 큰 문제는 없으므로 그냥 맘대로 경로를 잡아보겠다.

이제 이 경로를 구성하는 간선의 잔여 용량 중 가장 작은 것을 찾아야 한다. (왜냐하면 지금 s->a->b->t 경로에서 b->t는 잔여 용량이 2, s->a는 1인데 어차피 잔여 용량이 가장 작은 쪽에 맞춰줘야 하기 때문이다.)
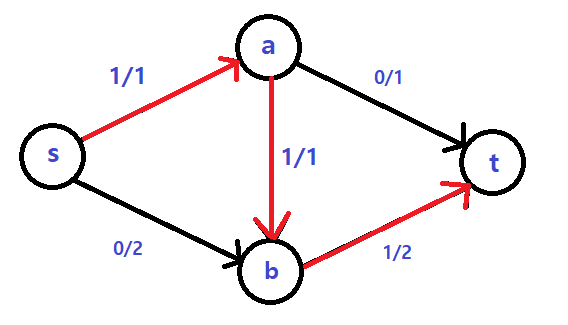
그렇게 찾은 작은 잔여 용량만큼을 흘려보낸다.

자, 이제 앞에서 말한 1~2단계가 끝났다. 여기서 구한 유량 1을 더해준 후 다시 1단계로 돌아가자.

이번엔 s->b->t라는 경로를 찾았다.

아까와 같이 가장 작은 잔여용량인 1만큼 흘려보낸다. (이제 전체 유량을 다시 1 더하면 2가 된다)

개인적으로 아래 문단이 포드 풀커슨을 이해하는 데 가장 중요한다고 생각한다.
자, 더 이상 유량을 흘려보낼 수 있는가? 일반적인 방법으로는 불가능하다. 왜냐하면 s->a의 잔여 용량이 0이고, s->b로 흘려보내도 b->t의 잔여 용량이 0이기 때문이다. 하지만 반대칭성을 생각했을 때는 b->a로 아까 흘렸던 유량을 거꾸로 되돌릴 수 있고, 거꾸로 유량을 되돌렸을 때 아까와는 다른 경로를 찾는다면 사실 맨 처음에 s->a->b->t로 잡았던 경로는, s->a->t로도 같은 유량을 흘릴 수 있었던 것이다! 그러면 이전에 미처 생각하지 못했던 "s->a->t라는 경로를 새로 발견했으므로" 최대 유량이 증가한다. 이제 다시 1만큼의 유량을 흘려보낸다.


이제 잔여 네트워크에서 s와 t를 연결할 수 있는 방법이 존재하지 않기 때문에 (더 이상 유량을 늘릴 수 없기 때문에) 포드 풀커슨 알고리즘은 종료된다.
맨 처음 발견한 s->a->b->t의 경로든, 나중에 s->a->b->t를 s->a->t라는 새로 발견한 경로든 간에 이 경로를 새로 발견함으로써 네트워크에 흐르는 유량이 증가하였기 때문에 이러한 경로를 증강 경로(augumenting path)라고 한다. 포드 풀커슨 알고리즘을 다시 요약하면 "잔여 네트워크에서 증강 경로가 더 이상 존재하지 않을 때까지 유량을 흘려보내는" 알고리즘이다.
구현
증명
포드 풀커슨 알고리즘은 항상 최대 유량을 구할 수 있는가? (Proof of Correctness)
residual network에서 s에서 t로 향하는 경로를 찾는 것은 이 네트워크의 "augmenting path"를 찾는 것이고, augmenting path가 존재한다는 것은 유량을 그냥 흘려보내든 이전에 찾았던 경로를 바꿔서 흘려보내든 간에 "더 많은 유량"을 흘려보낼 수 있다는 의미이며, 반대로 생각하면 "augmenting path가 존재하지 않는다면 더 이상의 유량을 흘려보낼 여지가 없다"라는 의미가 된다. (물론 이 문장의 역이 성립하는 이유는 가정과 결론이 필요충분조건이기 때문이다.) 포드 풀커슨 알고리즘은 augmenting path가 존재하지 않을 때까지 반복되므로 포드 풀커슨 알고리즘을 통해 구한 유량이 최대 유량이 아니라면 모순이다.
포드 풀커슨 알고리즘은 항상 종료되는가? (Proof of Termination)
네트워크의 용량이 정수인 경우, augmenting path로 흘려보낼 수 있는 유량은 최소 1이다. 최대 유량이 F라고 한다면, 최악의 경우에도 F번만큼만 augmenting path를 찾기 때문에 포드 풀커슨 알고리즘은 항상 종료된다. (물론 F의 크기도 유한하다, 유량 네트워크가 유한하다면 말이다.)
포드 풀커슨 알고리즘의 시간 복잡도에 대한 증명
Proof of Termination에서 증명했듯, augmenting path를 어떻게 찾느냐에 관계없이 포드 풀커슨 알고리즘은 $O(EF)$안에 종료된다. 따라서 DFS, BFS로 구현할 때 이 알고리즘은 시간 복잡도가 $O(EF)$이다. 그런데, BFS로 구현할 때는 $O(EF)$, $O(VE^{2})$ 중 작은 것이라는 시간 복잡도를 갖는다. 한 번 증명해보자.
1. augmenting path를 찾을 때는 BFS를 사용하므로 $O(V + E) = O(E)$이다.
2. augmenting path는 최대 $O(VE)$번 찾는다. 이를 다시 증명해야 하는데, 하나의 augmenting path를 찾으면 적어도 한 개의 간선은 포화된다. 따라서 E개의 간선이 모두 포화되면 종료되는데, 각각의 간선은 최대 V번 만큼 포화될 수 있다. u->v가 포화되었다고 하자. 그런데 다시 v->u로 유량이 흐른 경우, $dist_{original}(s, v) + 1 \leq dist_{new}(s, v)$가 성립한다. 그런데 $dist(s, v)$는 V보다 커질 수 없으므로 최대 V번 만큼만 포화될 수 있다. (자세한 증명은 Introduction to Algorithms 3rd Edition, P750의 Theorem 26.8에서 볼 수 있다.)
따라서 $O(E) * O(VE) = O(VE^{2})$이다.
아, 그리고 포드 풀커슨 알고리즘이 아니라 포드 풀커슨 방법론이라고 불리는 이유는 augmenting path를 찾는 방법을 명시하지 않았기 때문이다. (BFS인지 DFS인지) BFS로 augmenting path를 찾는 것을 에드몬드 카프(Edmonds-Karp) 알고리즘이라고 한다.
그리고, 사실 DFS를 쓰는 것보다 BFS로 구현하는 게 항상 더 좋다. 왜냐하면 BFS로는 항상 최단 거리의 augmenting path를 찾을 수 있기 때문이다. 또한 최대 유량에 구애받지 않는다. ($O(VE^{2})$ 때문에)
요약 (이 글에서 다룬 것)
- 유량 네트워크가 무엇인가
- 네트워크 유량 문제는 무엇을 구하고자 하는가
- 포드 풀커슨 알고리즘의 동작 방식
- 용량, 유량, 잔여 용량의 관계
- 잔여 용량을 사용하는 이유
- augmenting path란 무엇인가와 그의 의미
- 포드 풀커슨 알고리즘의 유한성과 정당성
참고 사이트
https://en.wikipedia.org/wiki/Network_flow_problem
https://blog.naver.com/jh20s/221298145631
ps. 시간 복잡도 증명을 나정휘님께서 도와주셨습니다. 감사합니다.
댓글